Selina Concise Physics
Class 10 Physics
Chapter 2 Work, Energy and Power
Exercise 2(A)
1. Define work. When is work said to be done by a force?
Solution 1.
Work is said to be done only when the force applied on a body makes the body move. It is a scalar quantity.
2.How is the work done by a force measured when (i) force is in direction of displacement, (ii) force is at an angle to the direction of displacement?
2.How is the work done by a force measured when (i) force is in direction of displacement, (ii) force is at an angle to the direction of displacement?
Solution 2.
(i) When force is in direction of displacement, then work done , W = F x S
(ii) When force is at an angle θ to the direction of displacement, then work done, W= F S cos θ
3.A force F acts on a body and displaces it by a distance S in a direction at an angle Selina Solutions Icse Class 10 Physics Chapter - Work Energy And Power with the direction of force. (a) Write the expression for the work done by the force. (b) What should be the angle between force and displacement so that the work done is (i) zero, (ii) maximum?
3.A force F acts on a body and displaces it by a distance S in a direction at an angle Selina Solutions Icse Class 10 Physics Chapter - Work Energy And Power with the direction of force. (a) Write the expression for the work done by the force. (b) What should be the angle between force and displacement so that the work done is (i) zero, (ii) maximum?
Solution 3.
(a) When force is at an angle θ to the direction of displacement, then work done, W= F S cos θ
(b) (i) For zero work done, the angle between force and displacement should be 90o as cos 90o = 0
W = FS cos90o= FS x 0 = 0
(ii) For maximum work done, the angle between force and displacement should be 0o as cos0o = 1
Hence, W=FScos 0o=FS
4.A body is acted upon by a force. State two conditions when the work done is zero.
4.A body is acted upon by a force. State two conditions when the work done is zero.
Solution 4.
Two conditions when the work done is zero are:
- When there is no displacement (S = 0) and,
- When the displacement is normal to the direction of the force (θ = 90o).
5.State the condition when the work done by a force is (i) positive, (ii) negative. Explain with the help of examples.
Solution 5.
(i) If the displacement of the body is in the direction of force, then work done is positive.
Hence, W= F x S
For example: A coolie does work on the load when he raises it up against the force of gravity. The force exerted by coolie (=mg) and displacement, both are in upward direction.
(ii) If the displacement of the body is in the direction opposite to the force, then work done is negative.
Hence, W =- F x S
For example: When a body moves on a surface, the frictional forces between the body and the surface is in direction opposite to the motion of the body and so the work done by the force of friction is negative.
6.A body is moved in a direction opposite to the direction of force acting on it. State whether the work is done by the force or work is done against the force.
6.A body is moved in a direction opposite to the direction of force acting on it. State whether the work is done by the force or work is done against the force.
Solution 6.
Work is done against the force.
7.When a body moves in a circular path, how much work is done by the body? Give reason.
(Hint: The body is acted upon by the centripetal force).
7.When a body moves in a circular path, how much work is done by the body? Give reason.
(Hint: The body is acted upon by the centripetal force).
Solution 7.
When a body moves in a circular path, no work is done since the force on the body is directed towards the centre of circular path (the body is acted upon by the centripetal force), while the displacement at all instants is along the tangent to the circular path, i.e., normal to the direction of force.
8.A satellite revolves around the earth in a circular orbit. What is the work done by the satellite? Give reason.
8.A satellite revolves around the earth in a circular orbit. What is the work done by the satellite? Give reason.
Solution 8.
Work done by the force of gravity (which provides the centripetal force) is zero as the force of gravity acting on the satellite is normal to the displacement of the satellite.
9.State whether work is done or not by writing yes or no, in the following cases?
(a) A man pushes a wall.
(b) A coolie stands with a box on his head for 15 min.
(c) A boy climbs up 20 stairs.
9.State whether work is done or not by writing yes or no, in the following cases?
(a) A man pushes a wall.
(b) A coolie stands with a box on his head for 15 min.
(c) A boy climbs up 20 stairs.
Solution 9.
Work is done only in case of a boy climbing up a stair case.
10.
10.
Solution 10.
When a coolie carrying some load on his head moves, no work is done by him against the force of gravity because the displacement of load being horizontal, is normal to the direction of force of gravity.
11.The work done by a fielder when he takes a catch in a cricket match, is negative. Explain.
11.The work done by a fielder when he takes a catch in a cricket match, is negative. Explain.
Solution 11.
Force applied by the fielder on the ball is in opposite direction of displacement of ball. So, work done by the fielder on the ball is negative.
12.Give an example when work done by the force of gravity acting on a body is zero even though the body gets displaced from its initial position.
12.Give an example when work done by the force of gravity acting on a body is zero even though the body gets displaced from its initial position.
Solution 12.
When a coolie carries a load while moving on a ground, the displacement is in the horizontal direction while the force of gravity acts vertically downward. So the work done by the force of gravity is zero.
13.What are the S.I. and C.G.S. units of work? How are they related? Establish the relationship.
13.What are the S.I. and C.G.S. units of work? How are they related? Establish the relationship.
Solution 13.
S.I unit of work is Joule.
C.G.S unit of work is erg.
Relation between joule and erg :
1joule = 1N x 1m
But 1N = 105dyne
And 1m = 100 cm = 102 cm
Hence, 1 joule = 105dyne x 102cm
= 107dyne x cm = 107erg
Thus, 1 Joule = 107 erg
14.State and define the S.I. unit of work.
14.State and define the S.I. unit of work.
Solution 14.
S. I unit of work is Joule.
1 joule of work is said to be done when a force of 1 newton displaces a body through a distance of 1 metre in its own direction.
Previous
15.Express joule in terms of erg.
15.Express joule in terms of erg.
Solution 15.
Relation between joule and erg :
1 joule = 1N x 1m
But 1N = 105dyne
And 1m = 100 cm= 102 cm
Hence, 1 joule = 105dyne x 102cm
= 107dyne x cm = 107erg
Thus, 1 Joule = 107 erg
16.A body of mass m falls down through a height h. Obtain an expression for the work done by the force of gravity.
16.A body of mass m falls down through a height h. Obtain an expression for the work done by the force of gravity.
Solution 16.
Let a body of mass m fall down through a vertical height h either directly or through an inclined plane e.g. a hill, slope or staircase. The force of gravity on the body is F = mg acting vertically downwards and the displacement in the direction of force (i.e., vertical) is S=h. Therefore the work done by the force of gravity is
W = FS = mgh
17.A boy of mass m climbs up a stairs of vertical height h.
(a) What is the work done by the boy against the force of gravity?
(b) What would have been the work done if he uses a lift in climbing the same vertical height?
17.A boy of mass m climbs up a stairs of vertical height h.
(a) What is the work done by the boy against the force of gravity?
(b) What would have been the work done if he uses a lift in climbing the same vertical height?
Solution 17.
Let a boy of mass m climb up through a vertical height h either through staircase of using a lift. The force of gravity on the boy is F=mg acting vertically downwards and the displacement in the direction opposite to force (i.e., vertical) is S=-h. Therefore the work done by the force of gravity on the boy is
W= FS =-mgh
or,the work W=mgh is done by the boy against the force of gravity.
18.Define the term energy and state its S.I unit.
18.Define the term energy and state its S.I unit.
Solution 18.
The energy of a body is its capacity to do work. Its S.I unit is Joule (J).
19.What physical quantity does electron volt (eV) measure? How is it related to the S.I. unit of that quantity?
19.What physical quantity does electron volt (eV) measure? How is it related to the S.I. unit of that quantity?
Solution 19.
eV measures the energy of atomic particles.
1eV= 1.6 x 10-19J
20.Complete the following sentence:
1 J = _____ calorie.
20.Complete the following sentence:
1 J = _____ calorie.
Solution 20.
1 J = 0.24 calorie
21.Name the physical quantity which is measured in calorie. How is it related to the S.I unit of that quantity?
21.Name the physical quantity which is measured in calorie. How is it related to the S.I unit of that quantity?
Solution 21.
Calorie measures heat energy.
1calorie = 4.18 J
22.Define a kilowatt hour. How is it related to joule?
22.Define a kilowatt hour. How is it related to joule?
Solution 22.
1kWh is the energy spent (or work done) by a source of power 1kW in 1 h.
1kWh = 3.6 x 106J
23.Define the term power. State its S.I. unit.
23.Define the term power. State its S.I. unit.
Solution 23.
The rate of doing work is called power. The S.I. unit of power is watt (W).
24.State two factors on which power spent by a source depends. Explain your answer with examples.
24.State two factors on which power spent by a source depends. Explain your answer with examples.
Solution 24.
Power spent by a source depends on two factors:
(i) The amount of work done by the source, and
(ii) The time taken by the source to do the said work.
Example: If a coolie A takes 1 minute to lift a load to the roof of a bus, while another coolie B takes 2 minutes to lift the same load to the roof of the same bus, the work done by both the coolies is the same, but the power spent by the coolie A is twice the power spent by the coolie B because the coolie A does work at a faster rate.
25.Differentiate between work and power.
25.Differentiate between work and power.
Solution 25.
Solution 26.
Solution 27.
S.I unit of power is watt (W).
If 1 joule of work is done in 1 second, the power spent is said to be 1 watt.
28.(a) Name the physical quantity measured in terms of horse power.
(b) How is horse power related to the S. I. unit of power?
28.(a) Name the physical quantity measured in terms of horse power.
(b) How is horse power related to the S. I. unit of power?
Solution 28.
Horse power is another unit of power, largely used in mechanical engineering. It is related to the S.I unit watt as :
1 H.P =746 W
29.Differentiate between watt and watt hour.
29.Differentiate between watt and watt hour.
Solution 29.
Watt (W) is the unit of power, while watt hour (Wh) is the unit of work, since power x time = work.
30.Name the quantity which is measured in
(a) kWh
(b) kW
(c) Wh
(d) eV
30.Name the quantity which is measured in
(a) kWh
(b) kW
(c) Wh
(d) eV
Solution 30.
a. Energy is measured in kWh
b. Power is measure in kW
c. Energy is measured in Wh
d. Energy is meaused in eV
Concept insight: Energy has bigger units like kWh (kilowatt hour) and Wh (watt hour). Similarly bigger unit of power is kW (kilo watt).
The energy of atomic particles is very small, and hence, it is measured in eV (electron volt).
1(MCQ).One horse power is equal to:
a. 1000 W
b. 500 W
c. 764 W
d. 746 W
1(MCQ).One horse power is equal to:
a. 1000 W
b. 500 W
c. 764 W
d. 746 W
Solution 1 (MCQ).
746 W
2(MCQ).k Wh is the unit of:
a. Power
b. Force
c. Energy
d. None of these
2(MCQ).k Wh is the unit of:
a. Power
b. Force
c. Energy
d. None of these
Solution 2 (MCQ).
The unit kWh is the unit of energy.
Numericals
1.A body, when acted upon by a force of 10 kgf, gets displaced by 0.5 m. Calculate the work done by the force, when the displacement is (i) in the direction of force, (ii) at an angle of 60o with the force, and (iii) normal to the force. (g= 10Nkg-1)
Solution 1.
2.A boy of mass 40kg climbs up the stairs and reaches the roof at a height 8m in 5 s. Calculate:
(i) The force of gravity acting on the boy,
(ii)The work done by him against gravity,
(iii)The power spent by boy.
(take g= 10ms-2)
Solution 2.
3.A man spends 6.4 kJ energy in displacing a body by 64 m in the direction in which he applies force, in 2.5 s. Calculate: (i) the force applied and (ii) the power spent (in H.P) by the man.
Solution 3.
4.A weight lifter lifted a load of 200 kgf to a height of 2.5 m in 5 s. Calculate: (i) the work done, and (ii) the power developed by him. Take g =10N/kg-1.
Solution 4.
5.A machine raises a load of 750N through a height of 16m in 5 s. Calculate:
the energy spent by the machine.
the power of the machine if it is 100% efficient.
Solution 5.
6.An electric heater of power 3kW is used for 10h. How much energy does it consume?
Express your answer in (i) kWh (ii) joule.
Solution 6.
7.A water pump raises 50 litres of water through a height of 25m in 5 s. Calculate the power of the pump required.
(Take g= 10N kg-1 and density of water =1000kg m-3).
Solution 7.
8.A pump is used to lift 500kg of water from a depth of 80m in 10s. Calculate:
- The work done by the pump,
- The power at which the pump works, and
- The power rating of the pump if its efficiency is 40%. (Take g= 10m s-2).
Solution 8.
9.An ox can apply a maximum force of 1000N. It is taking part in a cart race and is able to pull the cart at a constant speed of 30m/s-1 while making its best effort. Calculate the power developed by the ox.
Solution 9.
Solution 10.
11.A boy weighing 350 N climbs up 30 steps, each 20 cm high in 1 minute. Calculate: (i) the work done, and (ii) the power spent.
Solution 11.
12.It takes 20 s for a person A of mass 50 kg to climb up the stairs, while another person B of same mass does the same in 15 s. Compare the (i) work done and (ii) power developed by the persons A and B.
Solution 12.
(i) The work done by persons A and B is independent of time. Hence both A and B will do the same amount of work. Hence,
(ii) Power developed by the person A and B is calculated as follows:
A takes 20 s to climb the stairs while B takes 15 s, to do the same. Hence B does work at a much faster rate than A; more power is spent by B.
Solution 13.
Exercise 2(B)
1.What are the two forms of mechanical energy?
Solution 1.
Two forms of mechanical energy are:
- Kinetic energy
- Potential energy
2.Name the form of energy which a wound up watch spring possesses.
Solution 2.
Elastic potential energy is possessed by wound up watch spring.
3.Name the type of energy (kinetic energy K or potential energy U) possessed in the following cases:
A moving cricket ball
A compressed spring
A moving bus
A stretched wire
An arrow shot out of a bow.
A piece of stone placed on the roof.
3.Name the type of energy (kinetic energy K or potential energy U) possessed in the following cases:
A moving cricket ball
A compressed spring
A moving bus
A stretched wire
An arrow shot out of a bow.
A piece of stone placed on the roof.
Solution 3.
(a) Kinetic energy (K)
(b) Potential energy (U)
(c) Kinetic energy (K)
(d) Potential energy (U)
(e) Kinetic energy (K)
(f) Potential energy (U)
4.Define the term potential energy of a body. Name its two forms and given one example of each.
4.Define the term potential energy of a body. Name its two forms and given one example of each.
Solution 4.
Potential energy: The energy possessed by a body by virtue of its specific position (or changed configuration) is called the potential energy.
Different forms of P.E. are as listed below:
1. Gravitational potential energy: The potential energy possessed by a body due to its position relative to the centre of Earth is called its gravitational potential energy.
Example: A stone at a height has gravitational potential energy due to its raised height.
2. Elastic potential energy: The potential energy possessed by a body in the deformed state due to change in its configuration is called its elastic potential energy.
Example: A compressed spring has elastic potential energy due to its compressed state.
5.Name the form of energy which a body may possess even when it is not in motion. Give an example to support your answer.
5.Name the form of energy which a body may possess even when it is not in motion. Give an example to support your answer.
Solution 5.
Potential energy is possessed by the body even when it is not in motion. For example: a stone at a height has the gravitational potential energy due to its raised position.
6.What is meant by gravitational potential energy? Derive an expression for it for a body placed at a height above the ground.
6.What is meant by gravitational potential energy? Derive an expression for it for a body placed at a height above the ground.
Solution 6.
Gravitational potential energy is the potential energy possessed by a body due to its position relative to the centre of earth.
For a body placed at a height above the ground, the gravitational potential energy is measured by the amount of work done in lifting it up to that height against the force of gravity.
Let a body of mass m be lifted from the ground to a vertical height h. The least upward force F required to lift the body (without acceleration) must be equal to the force of gravity (=mg) on the body acting vertically downwards. The work done W on the body in lifting it to a height h is
W= force of gravity (mg) x displacement (h)
= mgh
This work is stored in the body when it is at a height h in the form of its gravitational potential energy.
Gravitational potential energy U= mgh
7.Write an expression for the potential energy of a body of mass m placed at a height h above the earth's surface. State the assumptions made, if any.
7.Write an expression for the potential energy of a body of mass m placed at a height h above the earth's surface. State the assumptions made, if any.
Solution 7.
The work done W on the body in lifting it to a height h is
W= force of gravity (mg) x displacement (h)
=mgh
This work is stored in the body when it is at a height h in the form of its gravitational potential energy.
Gravitational potential energy U= mgh
8.What do you understand by the kinetic energy of a body?
8.What do you understand by the kinetic energy of a body?
Solution 8.
A body in motion is said to possess the kinetic energy. The energy possessed by a body by virtue of its state of motion is called the kinetic energy.
9.A body of mass m is moving with a velocity v. Write the expression for its kinetic energy.
9.A body of mass m is moving with a velocity v. Write the expression for its kinetic energy.
Solution 9.
Solution 10.
According to the work-energy theorem, the work done by a force on a moving body is equal to the increase in its kinetic energy.
11.A body of mass m is moving with a uniform velocity u. A force is applied on the body due to which its velocity increases from u to v. How much work is being done by the force?
11.A body of mass m is moving with a uniform velocity u. A force is applied on the body due to which its velocity increases from u to v. How much work is being done by the force?
Solution 11.
Body of mass m is moving with a uniform velocity u. A force is applied on the body due to which its velocity changes from u to v and produces an acceleration a in moving a distance S.Then,
Work done by the force= force x displacement
W = F x S———(i)
12.A light mass and a heavy mass have equal momentum. Which will have more kinetic energy?
[Hint: kinetic energy K=p2/2m where p is the momentum]
Solution 12.
Both the masses have same momentum p. The kinetic energy, K is inversely proportional to mass of the body.
Hence light mass body has more kinetic energy because smaller the mass, larger is the kinetic energy.
13.Two bodies A and B of masses m and M (M≫ m) have same kinetic energy. Which body will have more momentum?
13.Two bodies A and B of masses m and M (M≫ m) have same kinetic energy. Which body will have more momentum?
Solution 13.
Kinetic energy is related to momentum and mass as
p = √2mK
As the kinetic energy of both bodies are same, momentum is directly proportional to square root of mass.
Now, mass of body B is greater than that of body A.
Hence, body B will have more momentum than body A.
14.Name the three forms of kinetic energy and give one example of each.
14.Name the three forms of kinetic energy and give one example of each.
Solution 14.
The three forms of kinetic energy are:
- Translational kinetic energy- example: a freely falling body
- Rotational kinetic energy-example: A spinning top.
- Vibrational kinetic energy-example: atoms in a solid vibrating about their mean position.
15.State two differences between the potential energy and the kinetic energy.
Solution 15.
16.Complete the following sentences:
(a)The kinetic energy of a body is the energy by virtue of its _______.
(b)The potential energy of a body is the energy by virtue of its _______.
Solution 16.
(a) Motion.
(b) Position.
17.When an arrow is shot from a bow, it has kinetic energy in it. Explain briefly from where does it get its kinetic energy?
17.When an arrow is shot from a bow, it has kinetic energy in it. Explain briefly from where does it get its kinetic energy?
Solution 17.
When the string of a bow is pulled, some work is done which is stored in the deformed state of the bow in the form of its elastic potential energy. On releasing the string to shoot an arrow, the potential energy of the bow changes into the kinetic energy of the arrow which makes it move.
18.A ball is placed on a compressed spring. What form of energy does the spring possess? On releasing the spring, the ball flies away. Give a reason.
18.A ball is placed on a compressed spring. What form of energy does the spring possess? On releasing the spring, the ball flies away. Give a reason.
Solution 18.
The compressed spring has elastic potential energy due to its compressed state. When it is released, the potential energy of the spring changes into kinetic energy which does work on the ball if placed on it and changes into kinetic energy of the ball due to which it flies away.
19.In what way does the temperature of water at bottom of a waterfall differ from the temperature at the top? Explain the reason.
Solution 19.
When water falls from a height, the potential energy stored in water at a height changes into the kinetic energy of water during the fall. On striking the ground, a part of the kinetic energy of water changes into the heat energy due to which the temperature of water rises.
20.
20.
Solution 20.
Yes, when force is normal to displacement, no transfer of energy takes place.
21.Name the form of energy in which potential energy can change.
21.Name the form of energy in which potential energy can change.
Solution 21.
Kinetic energy.
22.Name six different forms of energy?
22.Name six different forms of energy?
Solution 22.
The six different forms of energy are:
- Solar energy
- Heat energy
- Light energy
- Chemical or fuel energy
- Hydro energy
- Nuclear energy
23.Energy can exist in several forms and may change from one form to another. For each of the following, state the energy changes that occur in:
(a) the unwinding of a watch spring
(b) a loaded truck when started and set in motion,
(c) a car going uphill,
(d) photosynthesis in green leaves,
(e) charging of a battery,
(f) respiration,
(g) burning of a match stick,
(h) explosion of crackers.
(a) the unwinding of a watch spring
(b) a loaded truck when started and set in motion,
(c) a car going uphill,
(d) photosynthesis in green leaves,
(e) charging of a battery,
(f) respiration,
(g) burning of a match stick,
(h) explosion of crackers.
Solution 23.
(a) Potential energy of wound up spring converts into kinetic energy.
(b) Chemical energy of petrol or diesel converts into mechanical energy (kinetic energy)
(c) Kinetic energy to potential energy
(d) Light energy changes into chemical energy
(e) Electrical energy changes into chemical energy
(f) Chemical energy changes into heat energy
(g) Chemical energy changes into heat and light energy
(h) Chemical energy changes into heat, light and sound energy
24.State the energy changes in the following cases while in use:
(a)Loudspeaker
(b)A steam engine
(c)Microphone
(d)Washing machine
(e)A glowing electric bulb
(f)Burning coal
(g)A solar cell
(h)Bio-gas burner
(i)An electric cell in a circuit
(j)A petrol engine of a running car
(k)An electric iron
(l)A ceiling fan
(m)An electromagnet.
24.State the energy changes in the following cases while in use:
(a)Loudspeaker
(b)A steam engine
(c)Microphone
(d)Washing machine
(e)A glowing electric bulb
(f)Burning coal
(g)A solar cell
(h)Bio-gas burner
(i)An electric cell in a circuit
(j)A petrol engine of a running car
(k)An electric iron
(l)A ceiling fan
(m)An electromagnet.
Solution 24.
(a) Electrical energy into sound energy
(b) Heat energy into mechanical energy
(c) Sound energy into electrical energy
(d) Electrical energy to mechanical energy
(e) Electrical energy into light energy
(f) Chemical energy to heat energy
(g) Light energy into electrical energy
(h) Chemical energy into heat energy
(i) Chemical energy into electrical energy
(j) Chemical energy to mechanical energy
(k) Electrical energy into heat energy
(l) Light energy into electrical energy
(m) Electrical energy into magnetic energy.
25.Is it practically possible to convert a form of energy completely into the other useful form? Explain your answer.
25.Is it practically possible to convert a form of energy completely into the other useful form? Explain your answer.
Solution 25.
No. This is because, whenever there is conversion of energy from one form to another apart of the energy is dissipated in the form of heat which is lost to surroundings.
1(MCQ).A body at a height possesses:
a. Kinetic energy
b. Potential energy
c. Solar energy
d. Heat energy
1(MCQ).A body at a height possesses:
a. Kinetic energy
b. Potential energy
c. Solar energy
d. Heat energy
Solution 1 (MCQ).
Potential energy
Hint: P.E. is the energy possessed by a body by virtue of its position.
2(MCQ).In an electric cell while in use, the change in energy is from:
a. Electrical to mechanical
b. Electrical to chemical
c. Chemical to mechanical
d. Chemical to electrical
2(MCQ).In an electric cell while in use, the change in energy is from:
a. Electrical to mechanical
b. Electrical to chemical
c. Chemical to mechanical
d. Chemical to electrical
Solution 2 (MCQ).
Chemical to electrical
Hint: When current is drawn from an electric cell, the chemical energy stored in it changes into electrical energy.
Numericals
1.Two bodies of equal masses are placed at heights h and 2h. Find the ratio of their gravitational potential energies.
Solution 1.
2.Find the gravitational potential energy of 1kg mass kept at a height of 5m above the ground if g =10ms-2.
Solution 2.
Mass , m=1kg
Height, h=5m
Gravitational potential energy = mgh
=1 x 10 x 5=50J
3.A box of weight 150kgf has gravitational potential energy stored in it equal to 14700J. Find the height of the box above the ground.
(Take g= 9.8N/kg-1).
Solution 3.
Gravitational potential energy=14700 J
Force of gravity = mg= 150 x 9.8N/kg= 1470N
Gravitational potential energy= mgh
14700 =1470 x h
h=10m
4.A body of mass 5 kg falls from a height of 10 m to 4 m. Calculate: (i) the loss in potential energy of the body, (ii) the total energy possessed by the body at any instant? (Take g = 10 ms-2).
4.A body of mass 5 kg falls from a height of 10 m to 4 m. Calculate: (i) the loss in potential energy of the body, (ii) the total energy possessed by the body at any instant? (Take g = 10 ms-2).
Solution 4.
5.Calculate the height through which a body of mass 0.5 kg should be lifted if the energy spent in doing so is 1.0 J. Take g = 10m/s-2.
Solution 5.
Mass =0.5 kg
Energy= 1 J
Gravitational potential energy= mgh
1=0.5 x10 x h
1=5h
Height, h= 0.2 m
6.A boy weighing 25 kgf climbs up from the first floor at height 3 m above the ground to the third floor at height 9 m above the ground. What will be the increase in his gravitational potential energy?
6.A boy weighing 25 kgf climbs up from the first floor at height 3 m above the ground to the third floor at height 9 m above the ground. What will be the increase in his gravitational potential energy?
(Take g=10 N kg-1).
Solution 6.
Force of gravity on boy=mg= 25 x 10 =250N
Increase in gravitational potential energy= Mg (h2-h1)
= 250 x (9-3)
=250 x6=1500 J
7.A vessel containing 50 kg of water is placed at a height 15m above the ground. Assuming the gravitational potential energy at ground to be zero, what will be the gravitational potential energy of water in the vessel? (g = 10ms-2).
7.A vessel containing 50 kg of water is placed at a height 15m above the ground. Assuming the gravitational potential energy at ground to be zero, what will be the gravitational potential energy of water in the vessel? (g = 10ms-2).
Solution 7.
Mass of water, m= 50kg
Height, h=15m
Gravitational potential energy= mgh
=50 x10 x 15
=7500 J
8.A man of mass 50 kg climbs up a ladder of height 10m. Calculate: (i) the work done by the man, (ii) the increase in his potential energy.
8.A man of mass 50 kg climbs up a ladder of height 10m. Calculate: (i) the work done by the man, (ii) the increase in his potential energy.
(g= 9.8m s-2).
Solution 8.
Mass of man=50kg
Height of ladder, h2=10m
(i) Work done by man =mgh2
=50 x 9.8 x10= 4900J
(ii) increase in his potential energy:
Height, h2= 10m
Reference point is ground, h1=0m
Gravitational potential energy= Mg (h2-h1)
= 50 x9.8x (10-0)
= 50 x 9.8 x10= 4900J
9.A block A, whose weight is 100N, is pulled up a slope of length 5m by means of a constant force F (=100N) as illustrated.
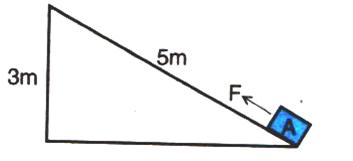
(a) What is the work done by the force F in moving the block A, 5m along the slope?
(b) What is the increase in potential energy of the block A?
(c) Account for the difference in the work done by the force and the increase in potential energy of the block.
9.A block A, whose weight is 100N, is pulled up a slope of length 5m by means of a constant force F (=100N) as illustrated.

(a) What is the work done by the force F in moving the block A, 5m along the slope?
(b) What is the increase in potential energy of the block A?
(c) Account for the difference in the work done by the force and the increase in potential energy of the block.
Solution 9.
F=150N
(a) Work done by the force in moving the block 5m along the slope =Force x displacement in the direction of force
=150 x 5=750 J.
(b) The potential energy gained by the block U =mgh where h =3m
=200 x 3=600 J
he potential energy gained by the block
(c) The difference i.e., 150 J energy is used in doing work against friction between the block and the slope, which will appear as heat energy.
10.Find the kinetic energy of a body of mass 1kg moving with a uniform velocity of 10m s-1.
10.Find the kinetic energy of a body of mass 1kg moving with a uniform velocity of 10m s-1.
Solution 10.
Solution 11.
If the speed is halved (keeping the mass same), the kinetic energy decreases, it becomes one-fourth (since kinetic energy is proportional to the square of velocity).
12.Two bodies of equal masses are moving with uniform velocities v and 2v. Find the ratio of their kinetic energies.
12.Two bodies of equal masses are moving with uniform velocities v and 2v. Find the ratio of their kinetic energies.
Solution 12.
Solution 13.
14.A ball of mass 0.5 kg slows down from a speed of 5m/s-1 to that of 3m/s-1. Calculate the change in kinetic energy of the ball.
Solution 14.
15.A canon ball of mass 500g is fired with a speed of 15m/s-1. Find: (i) its kinetic energy and (ii) its momentum.
Solution 15.
16.A body of mass 10 kg is moving with a velocity 20m s-1. If the mass of the body is doubled and its velocity is halved, find: (i) the initial kinetic energy, and (ii) the final kinetic energy.
Solution 16.
17.A truck weighing 1000 kgf changes its speed from 36 km/h-1 to 72 km/h-1 in 2 minutes. Calculate: (i) the work done by the engine and (ii) its power.
(g =10 m/s-2)
Solution 17.
18.A body of mass 60 kg has the momentum 3000 kgm/s-1. Calculate: (i) the kinetic energy and (ii) the speed of the body.
Solution 18.
Solution 19.
20.How much energy is gained by a box of mass 20 kg when a man
(a) carrying the box waits for 5 minutes for a bus?
(b) runs carrying the box with a speed of 3 m/s-1 to catch the bus?
(c) raises the box by 0.5 m in order to place it inside the bus? (g=10 m/s-2)
Solution 20.
21.A bullet of mass 50g is moving with a velocity of 500m/s-1. It penetrates 10 cm into a still target and comes to rest. Calculate: (a) the kinetic energy possessed by the bullet, and (b) the average retarding force offered by the target.
Solution 21.
22.A spring is kept compressed by a small trolley of mass 0.5 kg lying on a smooth horizontal surface as shown. When the trolley is released, it is found to move at a speed of v = 2 m/s-1. What potential energy did the spring possess when compressed?
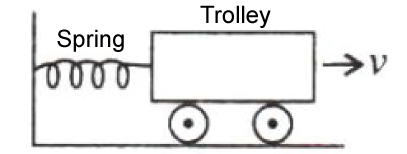
Solution 22.
Exercise 2(C)
1.State the Principle of conservation of energy.
Solution 1.
According to the law of conservation of energy, energy can neither be created nor can it be destroyed. It only changes from one form to another.
2.What do you understand by the conservation of mechanical energy? State the condition under which the mechanical energy is conserved.
2.What do you understand by the conservation of mechanical energy? State the condition under which the mechanical energy is conserved.
Solution 2.
According to the law of conservation of mechanical energy, whenever there is an interchange between the potential energy and kinetic energy, the total mechanical energy (i.e., the sum of kinetic energy K and potential energy U) remains constant i.e., K + U = constant when there are no frictional forces.
Mechanical energy is conserved only when there are no frictional forces for a given system (i.e. between body and air). Thus, conservation of mechanical energy is strictly valid only in vacuum, where friction due to air is absent.
3.Name two examples in which the mechanical energy of a system remains constant.
3.Name two examples in which the mechanical energy of a system remains constant.
Solution 3.
Motion of a simple pendulum and motion of a freely falling body.
4.A body is thrown vertically upwards. Its velocity keeps on decreasing. What happens to its kinetic energy as its velocity becomes zero?
4.A body is thrown vertically upwards. Its velocity keeps on decreasing. What happens to its kinetic energy as its velocity becomes zero?
Solution 4.
Kinetic energy of the body changes to potential energy when it is thrown vertically upwards and its velocity becomes zero.
5.A body falls freely under gravity from rest. Name the kind of energy it will possess
(a)At the point from where it falls.
(b)While falling
(c)On reaching the ground.
5.A body falls freely under gravity from rest. Name the kind of energy it will possess
(a)At the point from where it falls.
(b)While falling
(c)On reaching the ground.
Solution 5.
(a) Potential energy
(b) Potential energy and kinetic energy
(c) Kinetic energy
6.Show that the sum of kinetic energy and potential energy (i.e., total mechanical energy) is always conserved in the case of a freely falling body under gravity (with air resistance neglected) from a height h by finding it when (i) the body is at the top, (ii) the body has fallen a distance x, (iii) the body has reached the ground.
6.Show that the sum of kinetic energy and potential energy (i.e., total mechanical energy) is always conserved in the case of a freely falling body under gravity (with air resistance neglected) from a height h by finding it when (i) the body is at the top, (ii) the body has fallen a distance x, (iii) the body has reached the ground.
Solution 6.
Let a body of mass m be falling freely under gravity from a height h above the ground (i.e., from position A). Let us now calculate the sum of kinetic energy K and potential energy U at various positions, say at A (at height h above the ground), at B (when it has fallen through a distance x) and at C (on the ground).
(i) At the position A (at height h above the ground):
Initial velocity of body= 0 (since body is at rest at A)
Hence, kinetic energy K =0
Potential energy U = mgh
Hence total energy = K + U= 0 + mgh =mgh—–(i)
(ii) At the position B (when it has fallen a distance x):
Thus from equation (i), (ii) and (iii), we note that the total mechanical energy i.e., the sum of kinetic energy and potential energy always remain constant at each point of motion and is equal to initial potential energy at height h.
7.A pendulum is oscillating on either side of its rest position. Explain the energy changes that take place in the oscillating pendulum. How does the mechanical energy remain constant in it? Draw necessary diagram.
7.A pendulum is oscillating on either side of its rest position. Explain the energy changes that take place in the oscillating pendulum. How does the mechanical energy remain constant in it? Draw necessary diagram.
Solution 7.
When the bob swings from A to B, the kinetic energy decreases and the potential energy becomes maximum at B where it is momentarily at rest.
From B to A, the potential energy again changes into the kinetic energy and the process gets repeated again and again.
Thus while swinging, the bob has only the potential energy at the extreme position B or C and only the kinetic energy at the resting position A. At an intermediate position (between A and B or between A and C), the bob has both the kinetic energy and potential energy, and the sum of both the energies (i.e., the total mechanical energy) remains constant throughout the swing.
8.A pendulum with bob of mass m is oscillating on either side from its resting position A between the extremes B and C at a vertical height h above A. What is the kinetic energy K and potential energy U when the pendulum is at positions (i) A, (ii) B and (iii) C?
8.A pendulum with bob of mass m is oscillating on either side from its resting position A between the extremes B and C at a vertical height h above A. What is the kinetic energy K and potential energy U when the pendulum is at positions (i) A, (ii) B and (iii) C?
Solution 8.
(a) At position A, pendulum has maximum kinetic energy and its potential energy is zero at its resting position. Hence, K=mgh and U= 0.
(b) At B, kinetic energy decreases and potential energy increases. Hence, K= 0 and U=mgh
(c) At C also, kinetic energy K= 0 and potential energy U=mgh.
9.Name the type of energy possessed by the bob of a simple pendulum when it is at (a) the extreme position, (b) the mean position, and (c) between the mean and extreme positions.
9.Name the type of energy possessed by the bob of a simple pendulum when it is at (a) the extreme position, (b) the mean position, and (c) between the mean and extreme positions.
Solution 9.
a) Extreme position: Potential energy
b) Mean position: Kinetic energy
c) Between mean and extreme: Both kinetic energy and potential energy
10.
10.
Solution 10.
The gradual decrease of useful energy due to friction etc. is called the degradation of energy.
Examples:
- When we cook food over a fire, the major part of heat energy from the fuel is radiated out in the atmosphere. This radiated energy is of no use to us.
- When electrical appliances are run by electricity, the major part of electrical energy is wasted in the form of heat energy.
1(MCQ).A ball of mass m is thrown vertically up with an initial velocity so as to reach a height h. The correct statement is:
a. Potential energy of the ball at the ground is mgh.
b. Kinetic energy to the ball at the ground is zero.
c. Kinetic energy of the ball at the highest point is mgh.
d. Potential energy of the ball at the highest point is mgh.
a. Potential energy of the ball at the ground is mgh.
b. Kinetic energy to the ball at the ground is zero.
c. Kinetic energy of the ball at the highest point is mgh.
d. Potential energy of the ball at the highest point is mgh.
Solution 1 (MCQ).
Potential energy of the ball at the highest point is mgh.
Hint: At the highest point, the ball momentarily comes to rest and thus its kinetic energy becomes zero.
2(MCQ).A pendulum is oscillating on either side of its rest position. The correct statement is :
It has only the kinetic energy at its each position.
It has the maximum kinetic energy at its extreme position.
It has the maximum potential energy at its mean position.
The sum of its kinetic and potential energy remains constant throughout the motion.
2(MCQ).A pendulum is oscillating on either side of its rest position. The correct statement is :
It has only the kinetic energy at its each position.
It has the maximum kinetic energy at its extreme position.
It has the maximum potential energy at its mean position.
The sum of its kinetic and potential energy remains constant throughout the motion.
Solution 2 (MCQ).
The sum of its kinetic and potential energy remains constant throughout the motion.
Hint: In accordance with law of conservation of mechanical energy, whenever there is an interchange between the potential energy and kinetic energy, the total mechanical energy remains constant.
Numericals
1.A ball of mass 0.20 kg is thrown vertically upwards with an initial velocity of 20m/s-1. Calculate the maximum potential energy it gains as it goes up.
Solution 1.
2.A stone of mass 500g is thrown vertically upwards with a velocity of 15m/s-1. Calculate: (a) the potential energy at the greatest height, (b) the kinetic energy on reaching the ground (c) the total energy at its half way point.
Solution 2.
Solution 3.
(a)Potential energy of the ball =mgh
=2 x 10 x 5=100J
(b)Kinetic energy of the ball just before hitting the ground = Initial potential energy= mgh=2x10x5=100J
(c)Mechanical energy converts into heat and sound energy.
4.The diagram given below shows a ski jump.A skier weighing 60kgf stands at A at the top of ski jump. He moves from A and takes off for his jump at B.
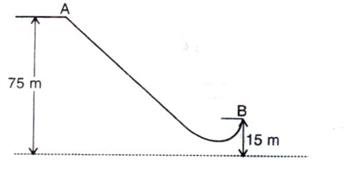
(a)Calculate the change in the gravitational potential energy of the skier between A and B.
(b)If 75% of the energy in part (a) becomes the kinetic energy at B, calculate the speed at
which the skier arrives at B.
(Take g = 10 m s-2).
4.The diagram given below shows a ski jump.A skier weighing 60kgf stands at A at the top of ski jump. He moves from A and takes off for his jump at B.

(a)Calculate the change in the gravitational potential energy of the skier between A and B.
(b)If 75% of the energy in part (a) becomes the kinetic energy at B, calculate the speed at
which the skier arrives at B.
(Take g = 10 m s-2).
Solution 4.
5.A hydro electric power station takes its water from a lake whose water level is 50m above the turbine. Assuming an overall efficiency of 40%, calculate the mass of water which must flow through the turbine each second to produce power output of 1MW.
(g=10 m s-2).
Solution 5.
Solution 6.

- Get link
- X
- Other Apps
Labels
Class 10 ICSE Physics
Labels:
Class 10
ICSE Physics
- Get link
- X
- Other Apps









































Comments
Post a Comment
This site is all about helping you kids study smart because for Gen Z, studying "hard" is not enough. If you feel there is any way I could improve my posts or if you have any random suggestion that might help make this more kid friendly, please don't hesitate to drop in a comment!
Be sure to check back for my response if you've asked me a question or requested a clarification through the comment section because I do make every effort to reply to your comments here.